Compartida por: Sandra Cara
0 votos
| 16554 | Planeación Interactiva de educación básica | ||||||||||
| Nivel escolar | Secundaria | Grado escolar | 3er grado | Campo y Asignatura | Matemáticas | Módulo | III | Semana | 30 | Sesión | 1 |
| Ejes | Forma, Espacio y Medida | ||||||||||
| Temas | Figuras y cuerpos geométricos | Duración | 1 hora | ||||||||
| Aprendizaje Esperado | Resuelve problemas utilizando las razones trigonométricas seno, coseno y tangente. | ||||||||||
| Etapas | Tiempo sugerido | Secuencia didáctica | MED | Bibliografía | |||||||
| Inicio | 00:20 | 1. Ver el MED propuesto para retomar las razones trigonométricas. 2. Hacer hincapié en la manera de resolver problemas de aplicación. 3. Pedir a los alumnos que identifiquen qué procedimientos se siguen a partir de los distintos problemas. 4. Preguntar: a) ¿Cuándo se usa el seno? b) ¿Cuándo se usa el coseno? c) ¿Cuándo se usa la tangente? |

Cálculo de distancia con Trigonometría básica
|
Matemáticas 3, Correo del Maestro, de Rubén García Madero, et. al. México 2021, pp. 132-137. |
|||||||
| Desarrollo | 00:25 | 1. Resolver a los alumnos las dudas que tengan al respecto después de ver el vídeo del apartado de "Descubre". 2. Proyectar el MED, el cual que se sugiere es un truco que facilitará el aprendizaje, el procedimiento es bastante sencillo. El resultado va a ser la raíz de un número entre 2, y ese número es el que corresponde a la fila del sen o del cos (según queramos calcular el seno o el coseno) y a la columna del ángulo notable en cuestión. 3. Después tan solo tenemos que simplificar el resultado obtenido. 4. Resolver las dudas que puedan surgir. |

Trigonometría: aplicaciones en la vida real
|
||||||||
| Cierre | 00:15 | 1. Resolver los siguientes problemas: a) Calcular la altura a, de un árbol sabiendo que, si nos situamos 4 metros de la base del tronco, vemos la parte superior de su copa en un ángulo de 36.87º. (Respuesta: 3 m) b) Se desea sujetar un poste de 20 metros de altura con un cable que parte de la parte superior del mismo hasta el suelo de modo que forme un ángulo de 25º. Calcular el precio del cable si cada metro cuesta $7.5. (Respuesta: $354.93) |
|
||||||||
| Evalúa | Evaluar a los estudiantes considerando lo siguiente: • Identificar en un esquema sencillo los datos de un triángulo rectángulo. • Identificar la función trigonométrica que relaciona la información conocida y deseada. • Utilizar con precisión la calculadora para encontrar el ángulo que se busca. | ||||||||||
Compartida por: Sandra Cara
0 votos
| 20139 | Planeación Interactiva de educación básica | ||||||||||
| Nivel escolar | Secundaria | Grado escolar | 3er grado | Campo y Asignatura | Matemáticas | Módulo | III | Semana | 30 | Sesión | 2 |
| Ejes | Forma, Espacio y Medida | ||||||||||
| Temas | Figuras y cuerpos geométricos | Duración | 1 hora | ||||||||
| Aprendizaje Esperado | Resuelve problemas utilizando las razones trigonométricas seno, coseno y tangente. | ||||||||||
| Etapas | Tiempo sugerido | Secuencia didáctica | MED | Bibliografía | |||||||
| Inicio | 00:20 | 1. Ver el MED propuesto para dar introducción a las razones trigonométricas desde un punto de vista de la vida cotidiana. |

Cálculo de la tangente de un ángulo
|
Matemáticas 3, Correo del Maestro, de Rubén García Madero, et. al. México 2021, pp. 132-137. |
|||||||
| Desarrollo | 00:25 | 1. Resolver las dudas que los alumnos tengan al respecto después de ver el vídeo. 2. Solicitar a los alumnos que encuentren un “truco” que facilite el aprendizaje: 3. El “truco” es saber deducir la razón trigonométrica que se requiere para resolver cada problema:
Resaltar que con esto se tienen el seno y el coseno de los ángulos notables del primer cuadrante.
|

Problemas utilizando las razones trigonométricas seno, coseno y tangente
|
||||||||
| Cierre | 00:15 | 1. Responder los siguientes ejercicios:
|
|
||||||||
| Evalúa | Evaluar a los estudiantes considerando lo siguiente: • Identificar en un esquema sencillo los datos de un triángulo rectángulo. • Identificar la función trigonométrica que relaciona la información conocida y deseada. • Utilizar con precisión la calculadora para encontrar el ángulo que se busca. | ||||||||||
Compartida por: Sandra Cara
0 votos
| 20141 | Planeación Interactiva de educación básica | ||||||||||
| Nivel escolar | Secundaria | Grado escolar | 3er grado | Campo y Asignatura | Matemáticas | Módulo | III | Semana | 30 | Sesión | 3 |
| Ejes | Forma, Espacio y Medida | ||||||||||
| Temas | Magnitudes y medidas | Duración | 1 hora | ||||||||
| Aprendizaje Esperado | Formula, justifica y usa el teorema de Pitágoras. | ||||||||||
| Etapas | Tiempo sugerido | Secuencia didáctica | MED | Bibliografía | |||||||
| Inicio | 00:20 | 1. Recordar la clasificación de los triángulos por sus ángulos (rectángulo, acutángulo, obtusángulo, equiángulo) y por sus lados (isósceles, equilátero, escaleno). 2. Mostrar el video y pedir a los estudiantes que se enfoquen en las partes del triángulo rectángulo y memoricen sus nombres. 3. Solicitar a los alumnos que tracen en su cuaderno un esquema de un triángulo rectángulo en el que identifiquen cuáles son los catetos y cuál es la hipotenusa. |

Catetos e hipotenusa
|
Matemáticas 3, Correo del Maestro, de Rubén García Madero, et. al. México 2021, pp. 138-141. |
|||||||
| Desarrollo | 00:25 | 1. Explicitar en el pizarrón con apoyo del triángulo rectángulo dibujado la desigualdad del triángulo sin indicar su representación algebraica (a+b>c, donde c es la hipotenusa). 2. Preguntar: ¿se cumple para cualquier triángulo? 3. Pedir a los alumnos que tracen 5 triángulos en distintas posiciones y de diferentes tamaños. Después indicarles que verifiquen la desigualdad del triángulo. 4. Preguntar: ¿Sólo se cumple para triángulos rectángulos o para cualquier triángulo? 5. Después de que respondan y entre todos lleguen a un acuerdo, cuestionar lo siguiente:
6. Guiar al grupo para que lleguen a: a+b>c. |
|
||||||||
| Cierre | 00:15 | 1. Solicita que observen con atención el video o presenta el ejercicio en el pizarrón explicando la deformación del triángulo al modificar la magnitud del ángulo entre dos lados dados. 2.Permite que los alumnos descubran la relación entre los otros dos lados con el lado restante para verificar que la expresión algebraica que obtuvieron funciona para cualquier triángulo. |

Teorema de la desigualdad del triángulo
|
||||||||
| Evalúa | Evaluar a los estudiantes considerando lo siguiente: • Identificar un triángulo rectángulo. • Identificar catetos e hipotenusa en un triángulo rectángulo. • Identificar la desigualdad triangular en cualquier triángulo. • Representar algebraicamente la desigualdad triangular. | ||||||||||
Compartida por: Sandra Cara
0 votos
| 20159 | Planeación Interactiva de educación básica | ||||||||||
| Nivel escolar | Secundaria | Grado escolar | 3er grado | Campo y Asignatura | Matemáticas | Módulo | III | Semana | 30 | Sesión | 4 |
| Ejes | Forma, Espacio y Medida | ||||||||||
| Temas | Magnitudes y medidas | Duración | 1 hora | ||||||||
| Aprendizaje Esperado | Formula, justifica y usa el teorema de Pitágoras. | ||||||||||
| Etapas | Tiempo sugerido | Secuencia didáctica | MED | Bibliografía | |||||||
| Inicio | 00:20 | 1. Presentar el tema de forma clara utilizando el MED, implementando materiales llamativos que permitan una mejor comprensión tanto teórica como práctica. |

Teorema de Pitágoras
|
||||||||
| Desarrollo | 00:25 | 1. Problematizar, mediante los ejercicios del MED de la vida diaria para que los estudiantes puedan resolverlas en clase:
|
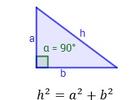
Problemas de aplicación del teorema de Pitágoras 1
|
Matemáticas 3, Correo del Maestro, de Rubén García Madero, et. al. México 2021, pp. 138-141. |
|||||||
| Cierre | 00:15 | 1. Pedir que presenten la solución de sus ejercicios y dar retroalimentación sobre el tema y la forma en que el teorema se lleva a la práctica. 2. Cuidar que realmente se llegue a la comprensión o retomar puntos base para aclarar dudas. |
|
||||||||
| Evalúa | Evaluar a los estudiantes considerando lo siguiente: • Fundamentar la fórmula del teorema de Pitágoras. • Identificar cada una de las partes que componen al teorema. • Aplicar la relación que existe entre las partes que componen al triángulo rectángulo en ejercicios y problemas de aplicación. | ||||||||||
Compartida por: Sandra Cara
0 votos
| 20160 | Planeación Interactiva de educación básica | ||||||||||
| Nivel escolar | Secundaria | Grado escolar | 3er grado | Campo y Asignatura | Matemáticas | Módulo | III | Semana | 30 | Sesión | 5 |
| Ejes | Forma, Espacio y Medida | ||||||||||
| Temas | Magnitudes y medidas | Duración | 1 hora | ||||||||
| Aprendizaje Esperado | Formula, justifica y usa el teorema de Pitágoras. | ||||||||||
| Etapas | Tiempo sugerido | Secuencia didáctica | MED | Bibliografía | |||||||
| Inicio | 00:20 | 1. Retomar el teorema de Pitágoras de forma clara. 2. Solicitar a los alumnos que enuncien el teorema con palabras y de manera algebraica: 3. Pedir a los alumnos que despejen una ecuación para obtener los catetos del triángulo. |
|
||||||||
| Desarrollo | 00:20 | 1. Problematizar, mediante los ejercicios del MED de la vida diaria para que los estudiantes puedan resolverlas en clase:
|

Problemas de aplicación del teorema de Pitágoras 2
|
Matemáticas 3, Correo del Maestro, de Rubén García Madero, et. al. México 2021, pp. 138-141. |
|||||||
| Cierre | 00:20 | 1. Pedir que presenten la solución de sus ejercicios y dar retroalimentación sobre el tema y la forma en que el teorema se lleva a la práctica. 2. Preguntar: ¿aplicar las fórmulas despejadas es la única manera de obtener cuánto miden los catetos? 3. Mostrar el siguiente video o presentar la información que se muestra en él para que los estudiantes noten que al resolver la ecuación también se puede ir despejando y no se trata sólo de la aplicación de una fórmula sin sentido. |

Cómo resolver problemas con el teorema de Pitágoras
|
||||||||
| Evalúa | Evaluar a los estudiantes considerando lo siguiente: • Fundamentar la fórmula del teorema de Pitágoras. • Identificar cada una de las partes que componen al teorema. • Aplicar la relación que existe entre las partes que componen al triángulo rectángulo en ejercicios y problemas de aplicación del teorema de Pitágoras. | ||||||||||
Regístrate y accede a todos los beneficios



